
asVoronoi3D¶
A procedural 3D Worley [Worley:1996:CTB:237170.237267] like noise shader, that outputs not only the resulting color, but the four nearest features to the evaluated point, their respective positions, and their cell color IDs. See also [Ebert:2002:TMP:572337].
Parameters¶
Color Parameters¶
- Color 1
- Primary cell color.
- Color 2
- Secondary cell color.
- Contrast
- Contrast between primary and secondary cell color.
Recursion Parameters¶
- Amplitude
- Controls the amplitute at each octave, including the starting iteration.
- Octaves
- Number of iterations to perform, higher values lead to increasing detail, but increased computational cost as well.
- Lacunarity
- Defines how large the gaps are in the cell noise with increasing octaves, higher values lead to higher gaps, lower values to small gaps.
- Persistence
- The persistence of the fractal is a gain factor to apply to the amplitude at each iteration, but it only has an effect when the shader is set to the mode pebbles.
Cell Parameters¶
- Density
- The density of the cells, with higher values resulting in a higher number of cells in the same area.
- Jittering
- How random the placement of the cells is, with low values resulting in a ordered grid of cells, and higher values resulting in aleatory placement of cells.
- Metric
- Which metric to choose to calculate the distance from cell to feature points. There are several to choose from, resulting in different types of patterns.
- Euclidian distance [1]
- Sum of square difference
- Tchebychev distance [2]
- Sum of absolute difference
- Akritean distance
- Minkowski metric [3]
- Karlsruhe metric [4]
The sum of the square difference is also known as the Manhattan metric [5].
The Minkowski metric is a generalized metric whose P parameter allows you to go from the Euclidian distance when P has a value of 2, to the Manhattan distance when P has a value of 1, and as P reaches infinity, it represents the Tchebychev metric.
The Akritean distance if a weighted mix of the Euclidian distance, and the Tchebychev distance.
The Karlsruhe metric, also known as Moscow metric, is a radial metric, returns radial sections from a cell at the center.
- Minkowski Parameter
- Controls the metric, with a value of 1 being the Manhattan distance, 2 being the Euclidian distance, and higher values tending to the Tchebychev metric as the parameter approaches infinity.
- Coverage
- The Akritean distance coverage, or the weighting mix between the Euclidian distance and the Tchebychev distance.
- Features Mode
- The features mode to use when computing the output color.
- Feature 1, or nearest feature from the cell
- Feature 2, or second nearest feature from the cell
- Feature 3, or third nearest feature from the cell
- Feature 4, or fourth nearest feature from the cell
- F1 + F2, or sum of first and second nearest features
- F2 - F1, or difference between second and first nearest features
- F1 * F2, or product of first and second nearest features
- F1 / F2, or division of first nearest feature by second nearest feature
- F1 ^ F2, nearest feature raised to the second nearest feature
- Pebbles, a mode that resembles pebbles
- Cell ID 1, the ID of the nearest feature to the cell
- Cell ID 2, the ID of the second nearest feature to the cell
- Cell ID 3, the ID of the third nearest feature to the cell
- Cell ID 4, the ID of the fourth nearest feature to the cell
Note
The unmodified features, points and their color IDs are also output from the shader, giving the user greater creative potential. The feature modes above are but a starting point.
Color Balance¶
The standard Maya color balance, gain, offset parameters. Please consult Maya’s documentation for more information on these controls.
Effects¶
The standard Maya effects parameters. Please consult Maya’s documentation for more information on these controls.
Coordinates¶
Typically, the placement 3d node’s placement matrix, which provides a placement matrix to transform the surface point providing the x,y,z coordinates. By default this point is the global primitive variable P, but the user can override this if needed.
Outputs¶
- Output Color
- The color resulting from ghe Features Mode choice.
- Output Alpha
- The alpha resulting from the Features Mode choice, usually luminance of the color only.
- Output Features
- An array of 4 floats, containing the four nearest features to the cell.
- Output Positions
- An array of 4 points, containing the center of the four nearest features to the cell.
- Output IDs
- An array of 4 colors, containing the color IDs of the four nearest features to the cell.
Warning
presently OSL does not allow connections from/to array elements, and appleseed-maya is not enabling the array outputs for now. This will be addressed in a future release.
Screenshots¶
Some examples of different metrics and feature output combinations used.








Footnotes
| [1] | The Euclidian distance or Euclidian metric, also known as 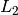 norm, is the straight line distance between two points in Euclidian space. norm, is the straight line distance between two points in Euclidian space. |
| [2] | The Chebyshev (or Tchebychev) distance, also known as Chessboard distance or 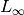 norm, is a metric on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension. norm, is a metric on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension. |
| [3] | The Minkowski distance, also known as 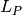 norm, is a metric which is a generalization of both the Euclidian distance and the Manhattan distance, being equal to the Manhattan distance when its p parameter is equal to 1, or equal to the Euclidian distance when its p parameter is equal to 2. On the limit as p approaches infinity, it is equal to the Chebyshev distance. norm, is a metric which is a generalization of both the Euclidian distance and the Manhattan distance, being equal to the Manhattan distance when its p parameter is equal to 1, or equal to the Euclidian distance when its p parameter is equal to 2. On the limit as p approaches infinity, it is equal to the Chebyshev distance. |
| [4] | In metric geometry, the Karlsruhe metric is a measure of distance that assumes travel is only possible along rays through the origin and circular arcs centered at the origin. |
| [5] | The Manhattan distance, also known as taxicab metric or 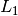 norm, is a metric in which the distance between two points is the sum of the absolute differences of their Cartesian coordinates. norm, is a metric in which the distance between two points is the sum of the absolute differences of their Cartesian coordinates. |
References
| [EMP+02] | David S. Ebert, F. Kenton Musgrave, Darwyn Peachey, Ken Perlin, and Steven Worley. Texturing and Modeling: A Procedural Approach. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 3rd edition, 2002. ISBN 1558608486. |
| [Wor96] | Steven Worley. A cellular texture basis function. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ‘96, 291–294. New York, NY, USA, 1996. ACM. URL: http://doi.acm.org/10.1145/237170.237267, doi:10.1145/237170.237267. |
